1.12 最大功率传递定理

本教程将学习最大功率传输定理（Maximum Power Transfer Theorem, MPTT）。这是电气工程领域中一个基本但重要的定律，它描述了实现最大功率传输（而不是最大效率）的必要条件。

最大功率传输定理

在任何电路中，电源提供的电能被传输到负载，在那里被转换为有用的工作。实际上，由于网络中的热效应和其他限制，负载处的功率会小于电源提供的总功率。因此，存在功率的提取和传输之间的差异。

负载的大小总是影响从电源传输到负载的功率，即负载电阻的任何变化都会导致传输到负载的功率发生变化。因此，最大功率传输定理确保了将最大功率传输到负载的理想条件。让我们看看“如何”实现这一点。

最大功率传输定理的表述

最大功率传输定理指出，在线性、双边直流网络中，当负载电阻等于电源的内部电阻时，负载获得最大功率。

如果是一个独立电压源，那么其串联电阻（内部电阻 $R_S$）；如果是一个独立电流源，那么其并联电阻（内部电阻 $R_S$）必须等于负载电阻 $R_L$，才能将最大功率传输到负载。

最大功率传输定理的证明

最大功率传输定理确保了负载电阻的值，使得传输到负载的功率最大。

考虑下图所示的直流双端网络（左侧电路）。通过使用网孔或节点电流方法获得负载吸收的功率表达式，然后对负载电阻 $R_L$ 求导，可以确定最大功率的条件。

这是一个相当复杂的过程。但在前面的教程中，我们已经看到复杂的网络部分可以用戴维宁等效电路替换，如下图所示。

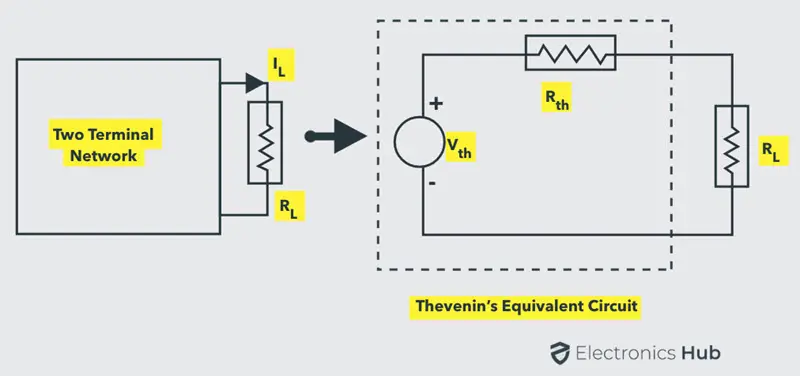
原双端电路被戴维宁等效电路替换，连接到可变负载电阻上。对于任何负载电阻值，通过负载的电流为：

从上述表达式可以看出，传输的功率取决于 $R_{TH}$ 和 $R_L$ 的值。然而，由于戴维宁等效电路是固定的，从这个等效源传输到负载的功率完全取决于负载电阻 $R_L$。为了找到 $R_L$ 的确切值，我们对 $P_L$ 关于 $R_L$ 求导，并将其设为零，如下所示：

因此，当负载电阻等于戴维宁电阻时，最大功率传输发生。将 $R_{TH} = R_L$ 代入上述方程，我们得到：

最大功率传输到负载的功率为：

从电源传输的总功率为：

$P_T = I_L^2 \times (R_{TH} + R_L)$ $P_T = 2 \times I_L^2 \times R_L \quad \quad \quad (2)$

因此，最大功率传输定理表达了负载获得最大功率的状态，即当负载电阻等于电路的戴维宁等效电阻时。下图显示了传输到负载的功率与负载电阻的关系曲线。

需要注意的是，当负载电阻为零时，传输的功率为零，因为在这种情况下负载两端没有电压降。同样，当负载电阻等于电路的内部电阻（或戴维宁等效电阻）时，功率达到最大。当负载电阻趋于无穷大时，功率再次为零，因为此时没有电流通过负载。

最大功率传输定理的功率传输效率

我们必须记住，这个定理只描述了最大功率传输，而不是最大效率。如果负载电阻小于电源电阻，那么负载处消耗的功率会减少，而大部分功率在电源处消耗，此时效率会降低。

考虑从电源传输的总功率方程（方程 2），其中功率在戴维宁等效电阻 $R_{TH}$ 上由电压源 $V_{TH}$ 消耗。

因此，在最大功率传输条件下，效率为：

$\text{效率} = \frac{\text{输出}}{\text{输入}} \times 100\%$ $= \frac{I_L^2 R_L}{2 I_L^2 R_L} \times 100\%$ $= 50\%$

因此，在最大功率传输条件下，效率为 50%，这意味着只有一半的生成功率被传输到负载。在其他条件下，传输到负载的功率百分比会更低，如下图所示的效率与最大功率传输曲线。

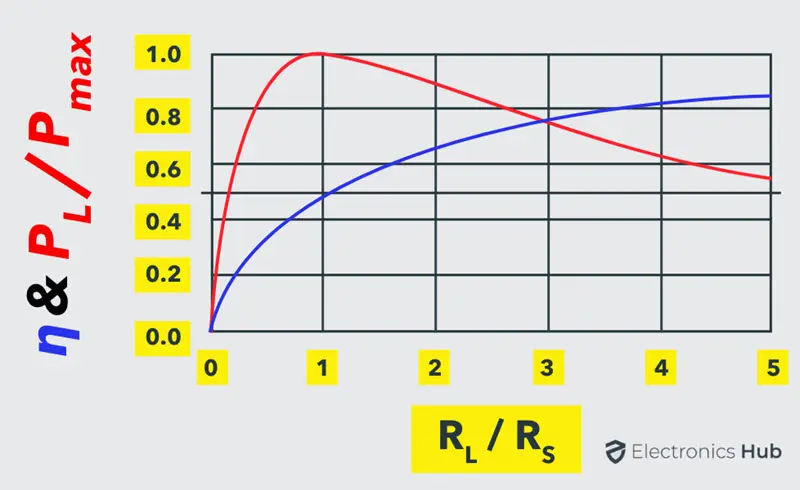
在某些应用中，将最大功率传输到负载比实现高效率更为重要，例如在放大器和通信电路中。

另一方面，在电力传输系统中，实现高效率比最大化功率传输更为重要。在这种情况下，负载电阻（远大于内部源电阻）被放置在负载上。尽管在这种情况下效率很高，但传输的功率会较少。

交流电路的最大功率传输定理

在有源网络中，可以表述为：当负载阻抗等于从负载端子看去的给定网络的等效阻抗的共轭复数时，负载获得最大功率。

考虑上述戴维宁等效电路，负载端子上的电流为：

$I = \frac{V_{TH}}{Z_{TH} + Z_L}$

其中 $Z_L = R_L + jX_L$，$Z_{TH} = R_{TH} + jX_{TH}$。

因此，

$I = \frac{V_{TH}}{(R_L + jX_L) + (R_{TH} + jX_{TH})}$ $I = \frac{V_{TH}}{(R_L + R_{TH}) + j(X_L + X_{TH})}$

传输到负载的功率为：

$P_L = I^2 \times R_L$ $P_L = \frac{V_{TH}^2 \times R_L}{(R_L + R_{TH})^2 + (X_L + X_{TH})^2} \quad \quad \quad (1)$

为了实现最大功率，上述方程的导数必须为零。经过简化后，我们得到：

$X_L + X_{TH} = 0$ $X_L = -X_{TH}$

将上述关系代入方程 (1)，我们得到：

$P_L = \frac{V_{TH}^2 \times R_L}{(R_L + R_{TH})^2}$

再次，为了实现最大功率传输，上述方程的导数必须为零。经过简化后，我们得到：

$R_L + R_{TH} = 2R_L$ $R_L = R_{TH}$

因此，在交流电路中，当 $R_L = R_{TH}$ 且 $X_L = -X_{TH}$ 时，电源将最大功率传输到负载。这意味着负载阻抗应等于电路的等效阻抗的共轭复数：

$Z_L = Z_{TH}$

其中 $Z_{TH}$ 是电路的等效阻抗的共轭复数。

最大功率传输为：

$P_{\text{MAX}} = \frac{V_{TH}^2}{4 R_{TH}} \quad \text{或} \quad \frac{V_{TH}^2}{4 R_L}$

最大功率传输定理在直流电路中的应用示例

考虑下图所示的电路，我们将确定从电源获得最大功率的负载电阻值，以及在最大功率传输条件下的最大功率。

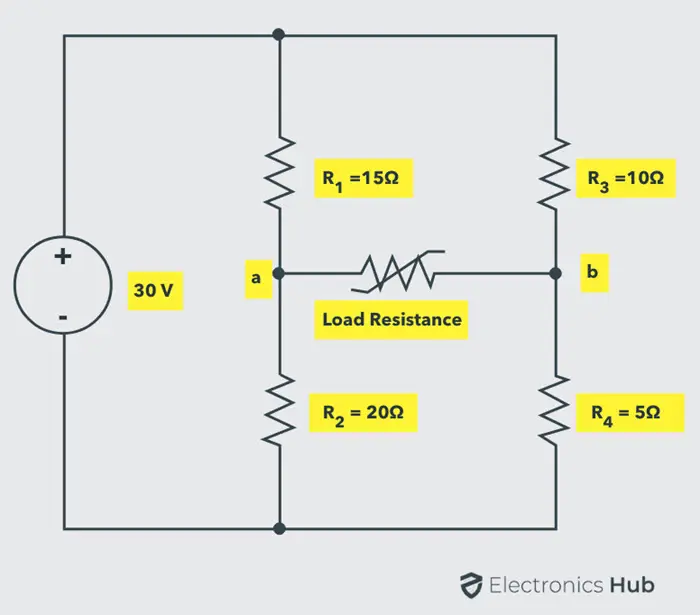
从负载端子 “a” 和 “b” 断开负载电阻。为了将给定电路表示为戴维宁等效电路，我们需要确定戴维宁电压 $V_{TH}$ 和戴维宁等效电阻 $R_{TH}$。

戴维宁电压或端子 ab 之间的电压为

$V_{ab} = V_a - V_b$ $V_a = V \times \frac{R_2}{R_1 + R_2} = 30 \times \frac{20}{20 + 15} = 17.14 \, \text{V}$ $V_b = V \times \frac{R_4}{R_3 + R_4} = 30 \times \frac{5}{10 + 5} = 10 \, \text{V}$ $V_{ab} = 17.14 - 10 = 7.14 \, \text{V}$ $V_{TH} = V_{ab} = 7.14 \, \text{伏特}$

通过将电源替换为其内部电阻（在此假设电压源的内部电阻为零，因此它成为短路）来计算戴维宁等效电阻 $R_{TH}$。

戴维宁等效电阻或端子 ab 之间的电阻为

$R_{TH} = R_{ab} = \left[ \frac{R_1 R_2}{R_1 + R_2} \right] + \left[ \frac{R_3 R_4}{R_3 + R_4} \right]$ $= \left[ \frac{15 \times 20}{15 + 20} \right] + \left[ \frac{10 \times 5}{10 + 5} \right]$ $= 8.57 + 3.33$ $R_{TH} = 11.90 \, \text{欧姆}$

将上述计算值重新连接负载电阻后的戴维宁等效电路如下图所示。

根据最大功率传输定理，负载电阻 $R_L$ 必须等于 $R_{TH}$，才能将最大功率传输到负载。

因此，

$R_L = R_{TH} = 11.90 \, \text{欧姆}$

在这种情况下传输的最大功率为：

$P_{\text{MAX}} = \frac{V_{TH}^2}{4 R_{TH}}$ $= \frac{(7.14)^2}{4 \times 11.90}$ $= \frac{50.97}{47.6} = 1.07 \, \text{瓦特}$

将最大功率传输应用于交流电路

下图所示的交流网络包含负载阻抗 $Z_L$，其感性和阻性部分都可以变化。因此，我们需要确定从电源传输的最大功率的负载阻抗值，以及最大功率的值。

为了找到负载阻抗的值，我们首先找到负载端子上的戴维宁等效电路。为了找到戴维宁电压，断开负载阻抗，如下图所示。

根据电压分配法则：

$V_{TH} = 20\angle0 \times \frac{j6}{4 + j6}$ $= 20\angle0 \times \frac{6\angle90}{7.21\angle56.3}$ $= 20\angle0 \times 0.825\angle33.7$ $V_{TH} = 16.5\angle33.7 \, \text{V}$

通过短路电压源，我们计算电路的戴维宁等效阻抗，如下图所示。

因此，

$Z_{TH} = \frac{4 \times j6}{4 + j6}$ $= \frac{4 \times 6\angle90}{7.21\angle56.3}$ $= 3.33\angle33.7 \, \text{或} \, 2.77 + j1.85 \, \text{欧姆}$

因此，负载端子上的戴维宁等效电路如下图所示。

因此，为了将最大功率传输到负载，负载阻抗的值应为

$Z_L = Z_{TH} = 2.77 - j1.85 \, \text{欧姆}$

传输的最大功率为：

$P_{\text{MAX}} = \frac{V_{TH}^2}{4 R_{TH}}$ $= \frac{(16.5)^2}{4 \times 2.77}$ $= \frac{272.25}{11.08} = 24.5 \, \text{瓦特}$

最大功率传输定理的实际应用

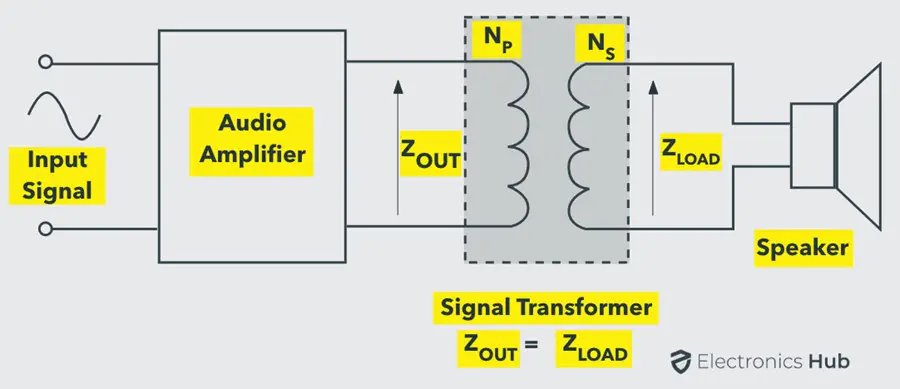
考虑一个实际的例子：一个阻抗为 8 欧姆的扬声器，由一个内部阻抗为 500 欧姆的音频放大器驱动。戴维宁等效电路也如图所示。

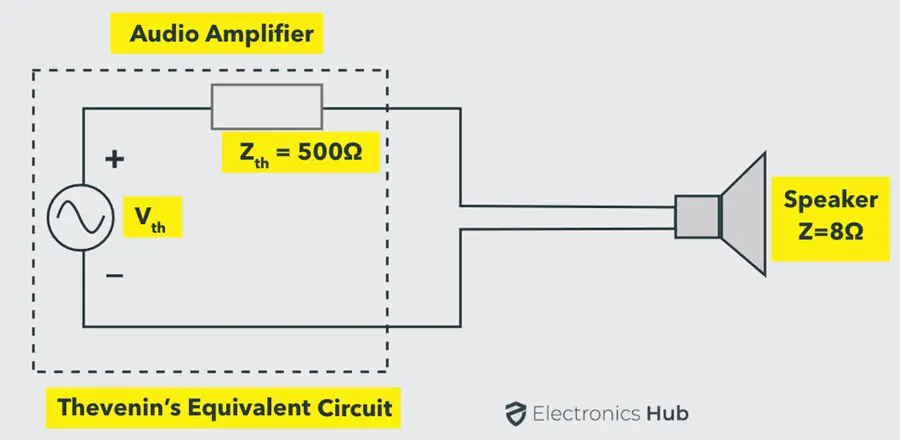
根据最大功率传输定理，如果负载阻抗为 500 欧姆（与内部阻抗相同），则负载处的功率达到最大。否则，需要将内部电阻改为 8 欧姆以实现最大功率传输条件。然而，这两种情况都无法改变。

因此，这是一个阻抗不匹配的情况，可以通过使用一个阻抗比为 500:8 的阻抗匹配变压器来克服。